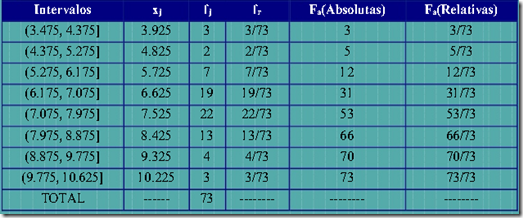
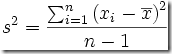Algo tan sencillo pero como nadie nace sabiendo, aquí un ejemplo de como hacerlo.
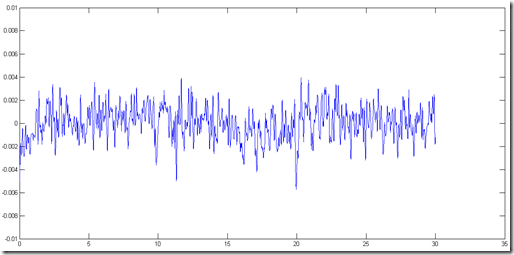
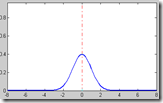
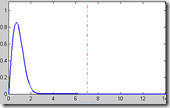
Ok, supongamos que tienen la señal que aparece en la figura de arriba, la cual por cierto, es una señal real de aceleración en la cintura de un sujeto de pie al que se le pidió que no se moviera. Como pueden ver, aun cuando no es notable a simple vista, hay mucho movimiento.
Nos interesa saber a que frecuencia está oscilando su cintura. Para ello, la forma más fácil es obtener la Transformada de Fourier.
Y eso es tan fácil como escribir lo siguiente en MATLAB
y=fft(d);
Y listo, tenemos nuestra FFT en la variable “y”. Ahora, si queremos verla en una gráfica y hacemos lo siguiente:
plot(y);
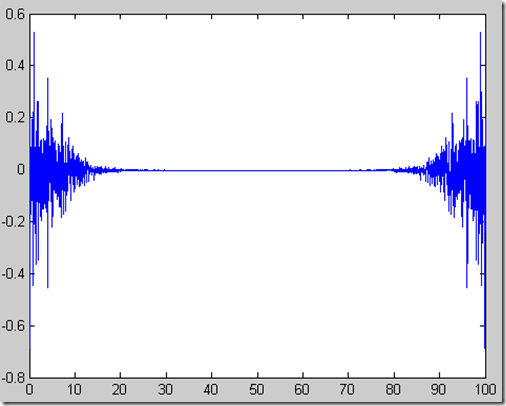
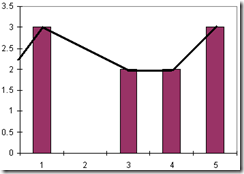
obtenemos
¿Qué es eso?
Bueno, lo que pasa es que hay que graficar esos datos junto con el vector de frecuencias. En esta caso muestreamos la señal a 100Hz y tenemos 3001 muestras, es decir, un poco más de 30 segundos así que hay que hacer un vector para eso:
f=linspace(0,100,length(y));
Ahora ya tenemos un vector con los datos del tiempo
Graficamos frecuencias (f) vs FFT y obtenemos
plot(f,y)
Sin embargo obtenemos un mensaje de alerta de MATLAB que dice:
Warning: Imaginary parts of complex X and/or Y arguments ignored.
Es decir, está omitiendo los datos imaginarios que generó la FFT, como ya se imaginaran, la FFT genera datos complejos que contienen la magnitud de la frecuencia y su fase. La fase en la parte compleja. Sin embargo, para esta aplicación sólo nos interesa la magnitud.
Además, observando la gráfica de arriba observamos que la señal se repite en el extremo opuesto, como un espejo. A nosotros sólo nos interesa la primera parte así que:
Sacamos la magnitud de la FFT y graficamos sólo la mitad
>> y=abs(y(1:fix(end/2)));
>> f=f(1:fix(end/2));
>> plot (f,y);
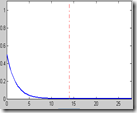
Ahora sí, ya tenemos la magnitud de las frecuencias de la señal.
Sin embargo aún hay que considerar que, la FFT entrega los resultados escalados por el número de total de muestras, así que para encontrar verdadera magnitud de la frecuencia debemos dividir entre el número total de muestras. Además, debido a la forma de calcular la FFT, también es necesario multiplicar el valor por 2. ver ecuación Euler
Haciendo la división entre 1500 y multiplicación por 2 tenemos:
>> y=2*y/3001;
>> plot (f,y);
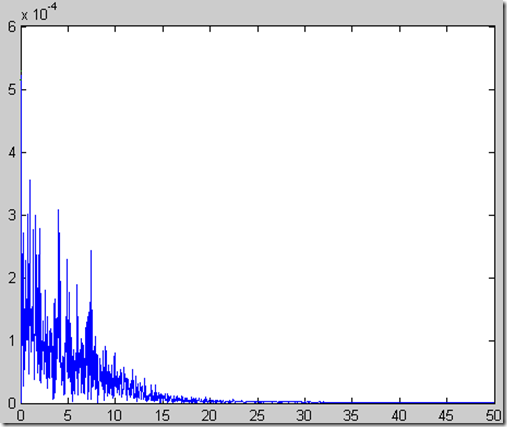
En el eje x tenemos la frecuencia (Hz) y en el eje Y, la amplitud de aceleración (g) para cada frecuencia.
Aquí una script que hace lo expuesto arriba
%script to calculate the frecuency behaviour by FFT and Pwelch
d=b1(:,1);
%Calculating the fft
yfft=2*abs(fft(d))/length(d); %Calcula la FFT, divide entre el numero de muestras y multiplica por 2
yfft=yfft(1:fix(end/2),:); %Deja solo la mitad de la FFT
t=linspace(0,50,length(yfft)); %Hace vector de frecuencias 50=100Hz/2
[yfft_max indx]=max(yfft); %Encuentra el pico maximo y su ubicacion
f_main=t(indx); %encuentra la ubicacion de acuerdo al vector de frecuencias
plot (t,yfft,f_main,yfft_max,'o'); % grafica la FFT con sus picos maximos encerrados en un circulo
La grafica con indica que la mayor concentración de energía de la señal esta en el rango de frecuencias de 0 a 20Hz.